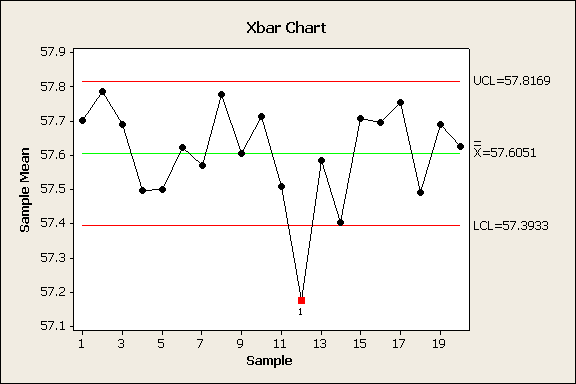
x_bar_관리도

만약 공정의 평균 <latex>\mu</latex>와 공정의 표준편차 <latex> \sigma </latex> 를 알 경우 <latex> \overline{X} </latex> 관리도의 중심선 및 관리한계선은 아래와 같다.

<latex> UCL = \mu + 3 \cdot \frac{\sigma}{\sqrt{n}} = \mu + A \cdot \sigma </latex>

<latex> CL = \mu </latex>

<latex> LCL = \mu - 3 \cdot \frac{\sigma}{\sqrt{n}} = \mu - A \cdot \sigma </latex>

단, 관리도 계수 $A = \frac{3}{\sqrt{n}}$이다. (관리도 계수표 (KS A 3201)참조)

만약 공정의 평균 <latex>\mu</latex>와 공정의 표준편차 <latex> \sigma </latex>를 모르는 경우에는 예비표본으로 부터 추정한 값을 이용하여 <latex>\overline{X}</latex> 관리도의 중심선 및 관리한계선을 아래와 같이 구한다.

공정의 평균 <latex> \mu </latex>의 추정치로 <latex>\overline{\overline{X}}</latex>를 이용

공정의 표준편차 <latex> \sigma </latex>의 추정치로 <latex>\overline{R} / d_{2}</latex>를 이용시

<latex> UCL = \overline{\overline{X}} + \frac{3}{\sqrt{n} \cdot d_{2}} \cdot \overline{R} = \overline{\overline{X}} + A_{2} \cdot \overline{R} </latex>

<latex> CL = \overline{\overline{X}} </latex>

<latex> LCL = \overline{\overline{X}} - \frac{3}{\sqrt{n} \cdot d_{2}} \cdot \overline{R} = \overline{\overline{X}} - A_{2} \cdot \overline{R} </latex>

공정의 평균 <latex>\mu</latex>의 추정치로 <latex>\overline{\overline{X}}</latex> 를 이용

공정의 표준편차 <latex>\sigma</latex>의 추정치로 <latex>\overline{s} / c_{4}</latex> 를 이용시

<latex>UCL = \overline{\overline{X}} + \frac{3}{\sqrt{n} \cdot c_{4}} \cdot \overline{s} = \overline{\overline{X}} + A_{3} \cdot \overline{s} </latex>

<latex>CL = \overline{\overline{X}} </latex>

<latex>LCL = \overline{\overline{X}} - \frac{3}{\sqrt{n} \cdot c_{4}} \cdot \overline{s} = \overline{\overline{X}} - A_{3} \cdot \overline{s} </latex>

단, 관리도 계수 <latex>A_{2} = \frac{3}{\sqrt{n} \cdot d_{2}}</latex>, <latex> A_{3} = \frac{3}{\sqrt{n} \cdot c_{4}}</latex>이다. (관리도 계수표 (KS A 3201)참조)

아래 표는 어떠한 기계부품을 제조하는 공정에서 5개의 부분군으로 이루어진 20개의 표본을 추출하여 만든 자료이다. 현재 이 자료를 바탕으로 <latex>\bar{X}-R</latex> 관리도의 관리한계선을 구하려고 한다.

(현재 기계부품 제조공정상의 실질적인 평균과 표준편차는 미지이다.)

부분군 번호	측정치					합계	평균	범위
부분군 번호	<latex>x_{1}</latex>	<latex>x_{2}</latex>	<latex>x_{3}</latex>	<latex>x_{4}</latex>	<latex>x_{5}</latex>	<latex>\Sigma x</latex>	<latex>\overline{x}</latex>	<latex>R</latex>
1	57.73	57.77	57.98	57.21	57.82	288.51	57.702	0.77
2	57.68	57.75	57.88	57.89	57.74	288.94	57.788	0.21
3	57.62	57.65	57.72	57.75	57.71	288.45	57.690	0.13
4	57.31	57.30	57.37	57.93	57.58	287.49	57.498	0.63
5	57.58	57.71	57.21	57.63	57.37	287.50	57.500	0.50
6	57.41	57.78	57.51	57.73	57.68	288.11	57.622	0.37
7	57.29	57.52	57.99	57.63	57.42	287.85	57.570	0.70
8	57.97	57.85	57.88	57.72	57.47	288.89	57.778	0.50
9	57.64	57.51	57.56	57.60	57.72	288.03	57.606	0.21
10	57.77	57.89	57.50	57.73	57.68	288.57	57.714	0.39
11	57.61	57.57	57.39	57.49	57.48	287.54	57.508	0.22
12	57.13	57.26	57.14	57.02	57.32	285.87	57.174	0.30
13	57.41	57.53	57.69	57.68	57.62	287.93	57.586	0.28
14	57.41	57.31	57.62	57.35	57.32	287.01	57.402	0.31
15	57.48	57.83	57.66	57.87	57.70	288.54	57.708	0.39
16	57.75	57.85	57.62	57.65	57.61	288.48	57.696	0.24
17	57.70	57.78	57.73	57.81	57.75	288.77	57.754	0.11
18	57.41	57.58	57.57	57.49	57.40	287.45	57.490	0.18
19	57.88	57.51	57.75	57.67	57.64	288.45	57.690	0.37
20	57.79	57.52	57.67	57.63	57.52	288.13	57.626	0.27

주어진 자료에서 공정 평균에 대한 관리도의 중심선 CL은 각 표본의 평균의 평균인 <latex>\overline{\overline{x}}</latex>이다.

<latex>CL = \overline{\overline{x}} = \frac{\sum_{i=1}^{20} \overline{x}_{i}}{20} = 57.6051</latex>

그리고 현재 표본에 대한 전체 평균 <latex>\overline{R}</latex> 은 아래와 같이 구할 수 있다.

<latex>\overline{R} = \frac{\sum_{i=1}^{20} R_{i}}{20} = 0.354</latex>

위에서 구한 CL과 <latex>\overline{R}</latex>를 이용해 아래와 값이 관리한계선 UCL과 LCL을 구할 수 있다.

(부분군 크기가 5일 경우 <latex>A_{2} = 0.577</latex> )

<latex>UCL=CL + A_{2} \overline{R} = 57.8169</latex>
<latex>LCL=CL - A_{2} \overline{R} = 57.3933</latex>

관리도

목차

X Bar 관리도

정의

중심선 및 관리한계선

예제1